任务与任务之间是个图,特征与特征之间也可以是个图
CVPR 2018 Best Paper | 任务学: 揭开任务迁移学习的秘密
Introduction
直觉告诉我们视觉任务之间存在着关联,但是这些关联是怎样的呢?这篇论文提出了一个完全通过计算的方法构建视觉任务的空间结构:
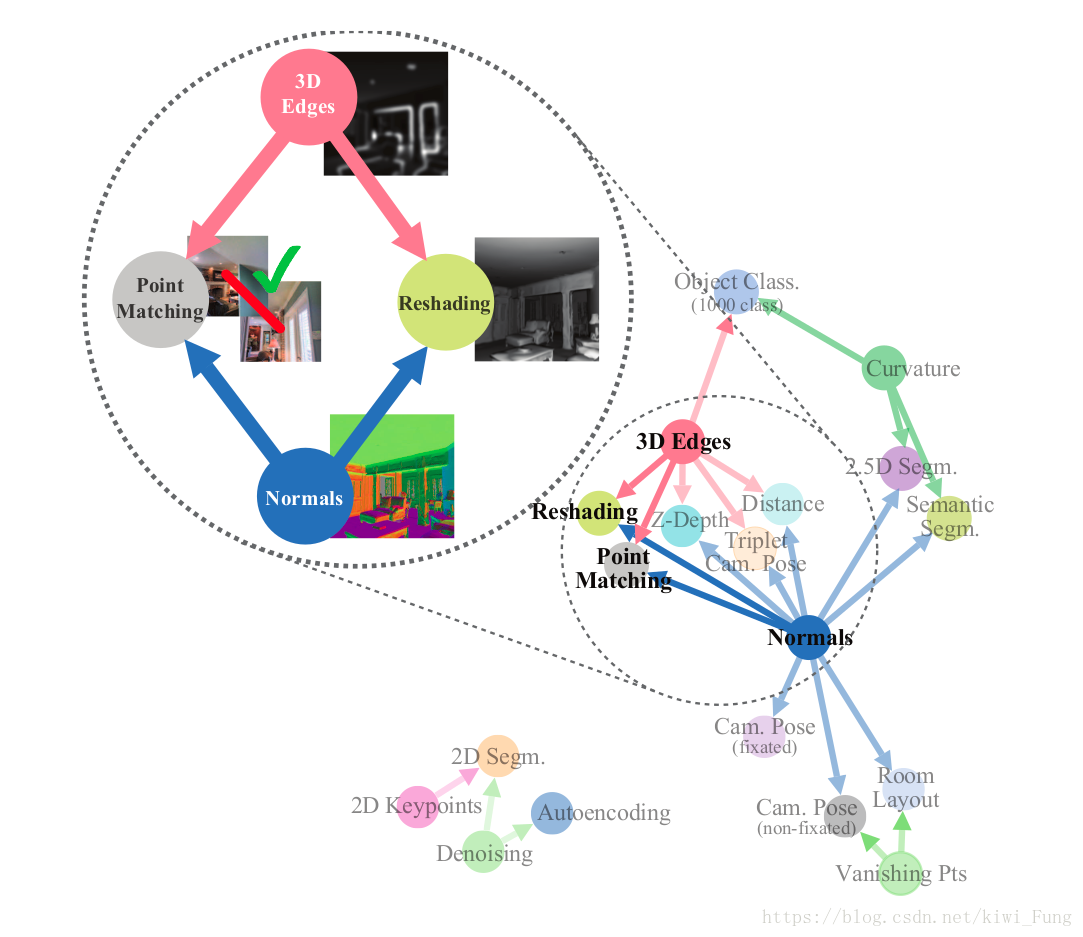
一个有向图,节点为任务,每一条的权重作为任务间的关联度。
当我们得知任务的边界的时候,知道哪些任务之间是有着比较好的关联度,那么利用迁移学习能够降低我们对于目标任务的标记数据的需求,从而降低我们对于大数据集的依赖,减少计算,同时使训练表现较好。而当前的深度学习忽视了这些任务之间的大量有用的关联,导致标记数据的大量需求。
本文的一些约定的Definition或者使用的名词
Structure(结构):通过计算发现的特定的某些任务可以提供可用信息另一个任务,包括提供的能力程度。(可以理解为有向图的一条边,以及其权重)
Binary Integer Programming: 0-1整数规划
通过计算出任务间的紧密关系矩阵(也就是基于一个任务是否充分容易地将其提取出来的表示用于其他任务的学习)这样的迁移是完全采样的,并且用了0-1整数规划来提取一个有效的全局训练策略。
由于这个方法是通过完全计算以及基于表示进行的,可以避免把自己的假设带入任务空间,确保提取出来的图是合理的,并且发现这种做法能够用远比单独训练一个任务少得多的数据来训练出目标任务。(例如我们容易认为深度迁移到曲面法线应该更容易,然而实际上反之更好)
Method
1.问题定义:
我们希望在有限的监督能力(由于资金/计算能力/时间等限制)下,最优化在一系列任务集合中的表现。
T :目标任务(我们希望训练出来/解决的任务)
S:源任务(我们已经训练好的任务,或者我们能够已有的充分的数据训练出来的任务)
V =T U S ,即所有任务的并集
T - T$\cap $S:不能被训练出来的但是想解决的(这就是我们希望做好的地方
T$\cap $S:能够被训练出来的而且是我们想解决的(这是极好的
S-T$\cap $S:可以被训练出来的,但是不是我们想解决的任务。(除非能够提高目标任务的训练结果,否则我们一般不理它)
Taskonomy (任务学): 一个计算发现的有向图,能够捕获从任意给定的一系列的任务当中提取其转移能力。
2.大概流程:
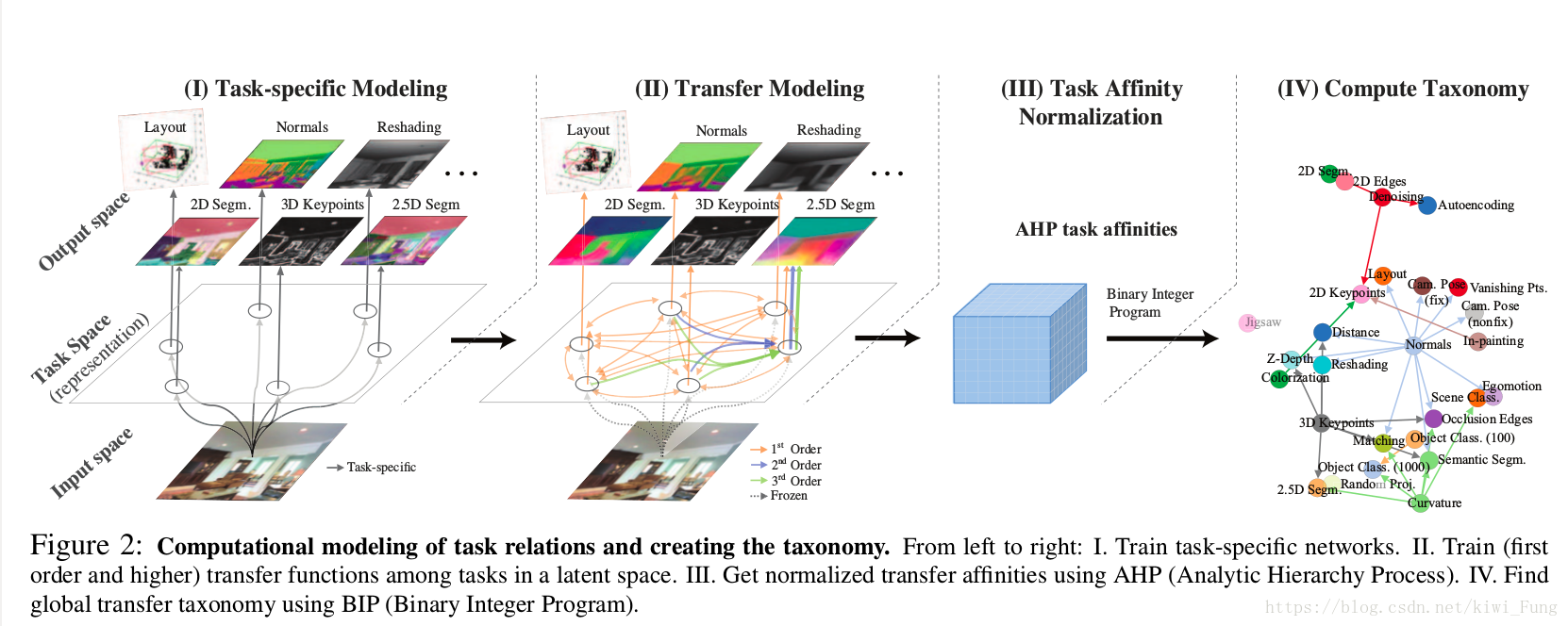
- 每一个任务建模训练
- 1v1,多v1的迁移学习建模
- 任务紧密程度的归一化
- 计算出Taskonomy
3.论文设计相关的内容
- 任务字典:本设计包括有26个任务,包括了计算机视觉的多个方面。(这只是一个样本集,而并不是全集)
- 数据集:400万张图片/600个建筑,每一张图片对于每一个任务都有对应的标记。
4. 具体流程
-
每一个特定任务的建模训练:
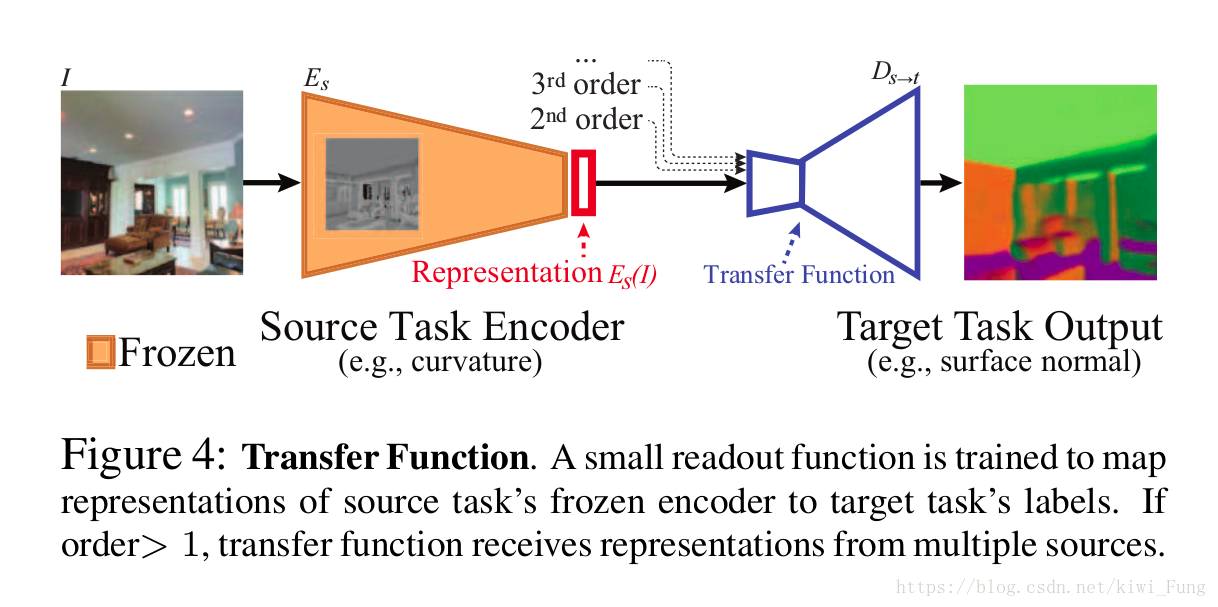
对于每一个 S 中的任务训练一个全监督的对于特定任务的网络。特定任务网络有一个编码器和解码器结构,编码器有足够的大小来提取特征,解码器有足够的能力来获得好的表现,但是相对于编码器而言会更小。
-
迁移训练建模
对于每一个源到目标任务,提出一个任务紧密程度的度量 D_s->t,
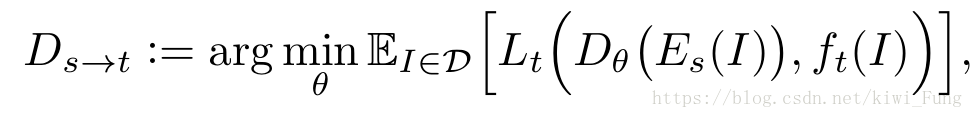
D: dataset
I: input
$E_S$(): 输入经过Encoder 之后的表示
$f_t$():输入的background输出
D_theta :以$\theta$ 为参数的read out function,就是从编码器之后的部分
$L_t$:预测与实际之间的损失
E_I\in D: 期望值
D_s->t就是通过最小化预测的结果与实际结果的损失的期望值,$\theta$为之参数,以此作为度量。
易得性:对于迁移来说,作为源,除了充足的信息,还有信息的易得性都是我们要考虑的内容。(因此评判迁移能力是在采用了低容量的模型来训练少量的数据下评估,使得所有的所有的迁移都是在充足的数据以及足够数据易得性下进行)
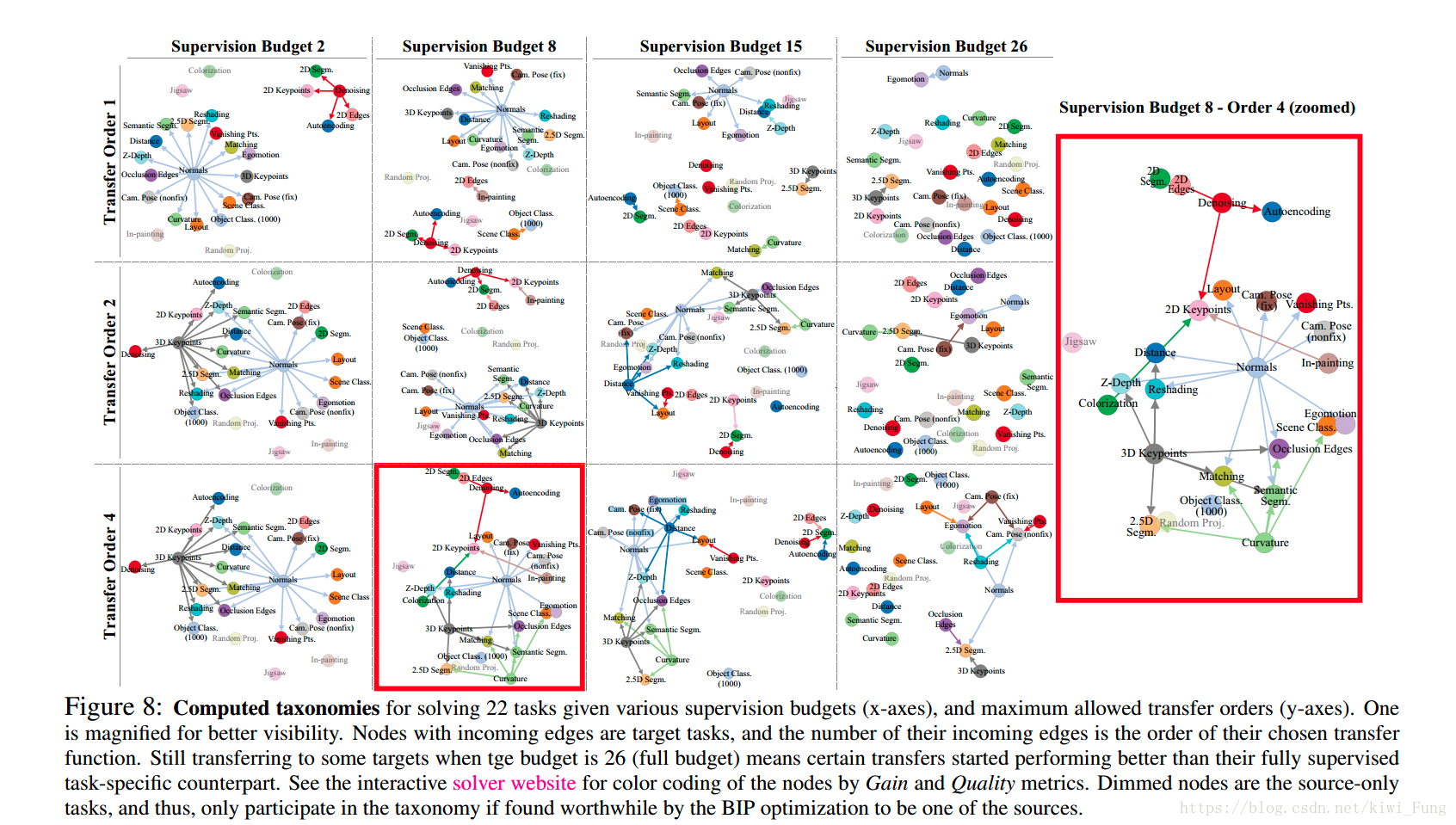
| 高阶迁移:当是采用多个任务迁移到一个任务的时候,容易发生组合爆炸,因为当需要进行k v 1 的迁移学习的时候,会有 | T | xC^k_ | S | 个可能。文中提出了采用Beam Search(宽度优先搜索+启发信息)的方法进行采样(当k<5的时候,采样的个数为5,当k>5的时候,采样个数为5个。)另外发现连续迁移(s->$t_1$->$t_2$对于迁移效果并没好处) |
-
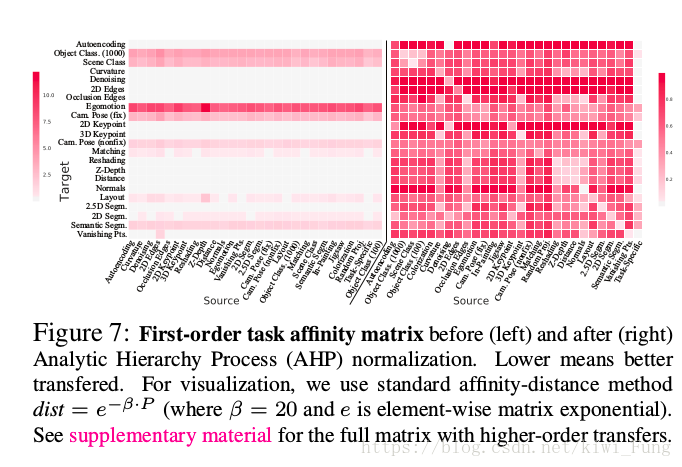
利用层次分析法对迁移的效果进构建成一个行归一化
通过迁移学习直接获得的数据,对于同一个目标任务,输出的$D_s->t$ 结果大小不一。直接的归一化,如果在输出的质量不同速度提升的时候,就不能够很好的表现出实际的情况。
3.0 然后把每一个源任务和目标任务对(i,j),在迁移学习之后,通过held-out方法取出测试集,对于每一个任务t,通过计算D_S_i->j>D_s_j->t构建成一个$W_t$.
3.1 首先通过的是clip(借助拉普拉斯平滑方法)将实际的产生的结果转化到范围为[0.001,0.999]
3.2 然后通过$W_t$’=$W_t$/$W_t^T$ 来得到这个,然后得出对于目标任务,我们可以比较得出到底$s_i$比$s_j$好多少倍。显然这里的矩阵内容对角线元素互为倒数。与AHP中的比较转移矩阵一致。
3.3 借鉴AHP中的方法,得到比较转移矩阵的最大特征值对应的特征向量,该特征向量stack得出的就是对于每一个任务其他任务提供信息的能力的矩阵。
-
计算全局的任务迁移能力图
全局的迁移策略来使整体的任务的表现最好,然后最小化监督的代价。其实就是对于子图进行优化,在满足不超出给定的监督代价的情况下,选出最理想的边和源节点。因此采用了0-1整数规划来解决。
这里实际上就是在第3步计算得出的图中作子图选择,挑选出合适的子图作为输出

然后对于定义一些参数:
$\gamma$: 监督的预算
$P$:任务间的紧密程度矩阵
$r_j$:目标任务的相对重要性
$l_i$ :对于i任务获得label的相对代价
对于0-1整数规划,实际上被一个向量x参数化,每一个转移的边和任务都被表示成一个0-1整数,然后这向量确定了哪些源和哪些迁移是被选择的。x表示的源和边,如果为1就被选择了。
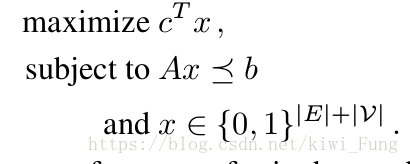

c作为表现评估系数,然后做的就是是受限于三个条件,实现最大化表现。对于c中的每一个元素,用户特定的目标任务重要程度$r_i$和每一个的独立的AHP表现$p_i$ ,$c_i$是两者的乘积。
A为三个受限条件:
- 每一个迁移和节点/任务都在子图中。
- 每一个目标任务都会有一个迁移进来
- 监督预算是不会超支
限制条件的数学表达:

Result
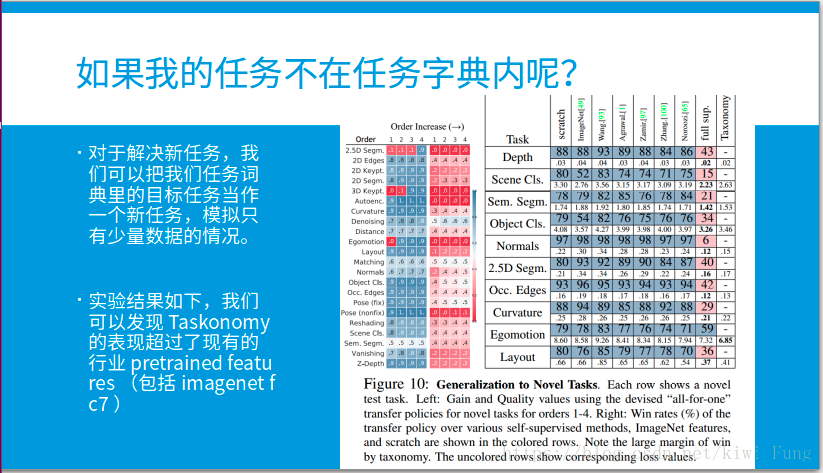
定义:Win Rate:test set中前者比后者效果好的比例。(胜率当然在0-1之间 迁移获利 (Gain) : 如果我们不进行迁移学习,我们只能基于少量的数据从零学习。迁移获利是指迁移学习相较于从零学习的胜率(见Ordinal Normalization部分)。 迁移质量 (Quality) : 用少量数据迁移学习相较于用大量数据从零学习的胜率

Reference
- https://zhuanlan.zhihu.com/p/38425434
- http://taskonomy.stanford.edu/
- TASKONOMY: Disentangling Task Transfer Learning
